電験三種の制御回路問題とは？機械科目合格に必要な基本知識を解説！

PID制御に関する問題について

初めに、もっとも基本的な制御方法とも言えるPID制御について解説します。実際の試験では言葉の定義などを問う問題が出題されることがあり、難しい計算を覚えなくても正解できるので、苦手な人もしっかりと勉強しておきましょう。

PID制御とは

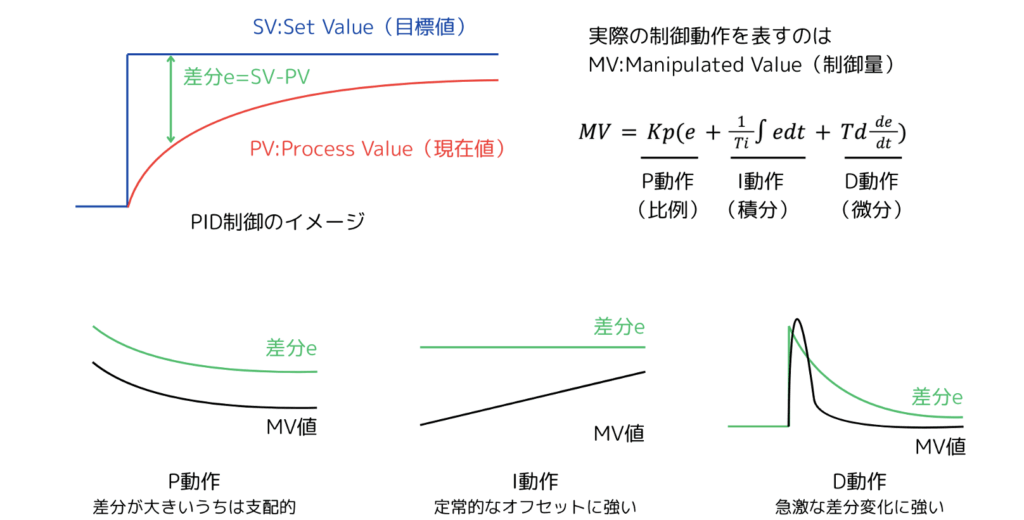
PID制御とは、比例（P動作）と積分（I動作）、および微分（D動作）の3つの要素を組み合わせて行う制御方法のことです。各動作の制御量は、制御対象の現在値と目標値の偏差によって決まり、P動作であれば偏差に比例した制御量となります。またI動作であれば偏差を時間積分した値に応じて制御量が決まり、D動作であれば偏差を時間微分した量に応じて制御量が決まります。一般的には最もシンプルなP制御が軸となり、必要に応じてI動作やD動作が組み合わせることで、最適な制御を目指します。

P動作とI動作の役割と制御イメージ

偏差が大きい初期状態では、制御量が偏差に比例するP動作が支配的となって制御を行います。ところが偏差が小さくなっていくと、P動作の制御も弱くなっていくため、システムによっては定常偏差（オフセット）が生じる場合もあります。そこで、偏差の時間積分に比例するI動作を組み合わせることで、定常状態におけるオフセットを減らし、現在値が目標値に合致するようにするのがPI制御です。

D動作の役割と制御イメージ

シンプルなシステムの制御であれば上述の通りPI制御だけで十分ですが、外乱の大きいシステムでは、外乱が入った際にPI制御だけでは対応しきれず、瞬間的に大きな偏差が生じることがあります。また温度制御など応答性が悪いシステムにおいても、目標値と現在値に乖離が生じることが多く、同じくPI制御だけで安定的に制御するのは難しいです。これらのシステムの制御において役立つのがD動作であり、偏差の瞬間的な変動に素早く対応することで、PI制御の弱点を克服することができます。

周波数伝達関数・ブロック線図・フィードバック制御・ボード線図

試験では、周波数伝達関数とブロック線図、フィードバック制御、およびボード線図について、複合的に知識を問われる問題も頻繁に出題されます。それぞれ基礎的な内容を抑えておきましょう。

周波数伝達関数とブロック線図とは

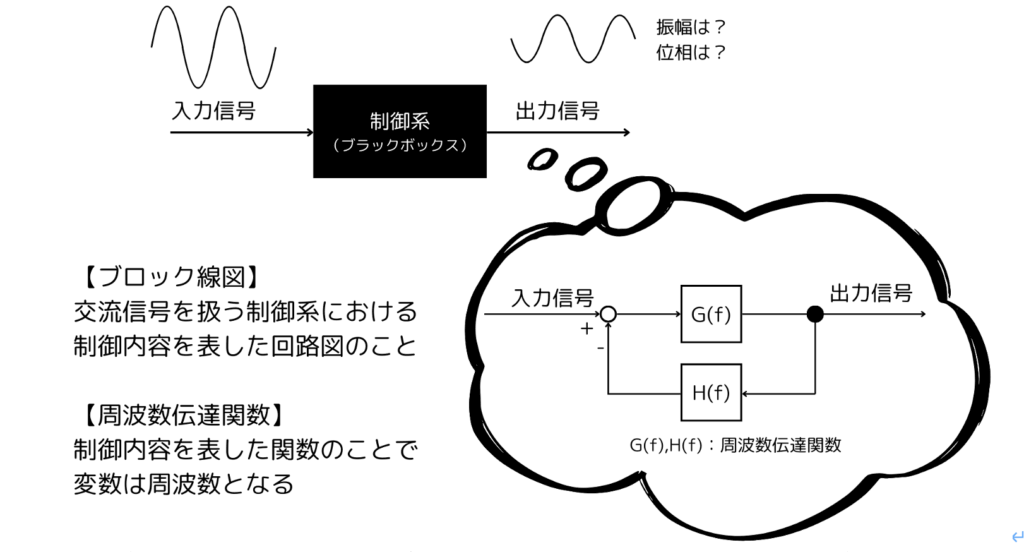
周波数伝達関数とは、制御系の振る舞いについて表した関数のことで、周波数が変数となります。一般的な交流信号は時間を変数とした関数で表すことが多いですが、入出力信号の振幅や位相が変動する制御回路では、時間が変数となる関数は扱いにくいため、周波数伝達関数が多く使用されるのです。

またブロック線図とは、制御系の制御内容や信号の流れなどを視覚的に分かりやすく表した回路図のことです。実際の試験では、ブロック線図の詳細を表した電気回路図をもとに周波数伝達関数を導き出す問題が多く出題されますが、電気回路の知識があれば解けるものがほとんどのため、解き方に慣れておきましょう。

フィードバック制御とシーケンス制御について

制御方式には幾つか種類がありますが、なかでもよく出てくる制御方式がシーケンス制御とフィードバック制御です。シーケンス制御とは、あらかじめ定められた手順に従い、逐次動作を行っていく制御方法のこと。決められた工程で洗浄する洗濯機の制御がわかりやすいかもしれませんね。

一方のフィードバック制御とは、制御対象の状態を監視しながら、必要に応じて制御量を最適化していく制御方法のことです。例えば現在の室温を計測しながら、目標とする温度との差分に応じて制御量を変えるエアコンの温度制御などが例として挙げられます。試験ではフィードバック制御を含んだブロック線図の周波数伝達関数を求める場面が多いため、計算式を暗記しておくと良いでしょう。

ボード線図について

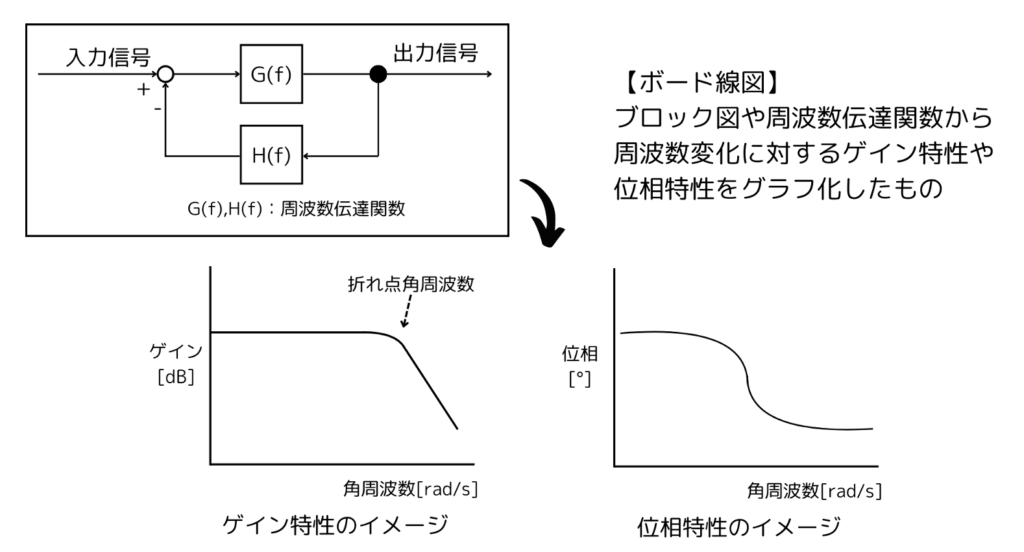
ボード線図とは、制御系の周波数特性を表したグラフのことで、扱う特性はゲイン特性と位相特性の2つに分かれます。ボード線図を用いることで、制御系の入力信号の周波数が変化した際に、出力信号の振幅や位相がどのように変化するかが視覚的に把握しやすくなるのがポイントです。

試験では実際にボード線図を作図するような問題はなく、与えられたブロック線図や回路図から、適切なボード線図や周波数特性を選択する問題が多いです。他の制御系の問題に比べると比較的難易度は高いものの、ゲインが急激に変化する折れ点角周波数の計算や、各周波数領域におけるゲイン特性を計算する方法が分かれば解くことができます。